Soziale Wohlfahrtsfunktionen

5.2.4 Das Optimum Optimorum

Bedingungen für das Optimum Optimorum

etzt ist es nur noch ein kleiner Schritt bis zum Ziel. Um ein eindeutiges Optimum für die Volkswirtschaft zu finden, werden das Bergsonsche Indifferenzkurvenschema und die Große Nutzenmöglichkeitskurve zur Deckung gebracht. Im Grunde ist dieser Schritt vom Auffinden des Haushaltsoptimums wenig verschieden. Die Bergsonschen Indifferenzkurven sind die "Präferenzen der Gesellschaft" und die Große Nutzenmöglichkeitskurve ist ihre Budgetrestriktion.

Abbildung 1

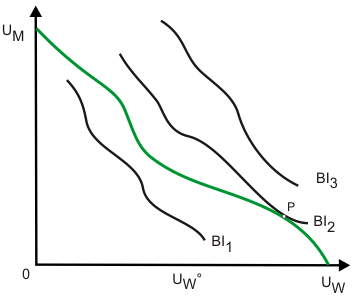
Offensichtlich wird die größtmögliche gesellschaftliche Wohlfahrt im Punkt P erreicht.

Zusammenfassend kann festgestellt werden:

Vom Gleichgewichtspunkt P aus, der auch bliss-point (bliss = Glückseligkeit) genannt wird, können alle Variablen des Modells eindeutig identifiziert werden. Zunächst findet man über die P zugehörige Nutzenmöglichkeitskurve im Punktsinn oder die Scitovsky-Indifferenzkurve den Produktionspunkt auf der Transformationskurve. In der darunter eingezeichneten Edgeworth-Box erkennt man die personelle Güterverteilung und im Vierfelderdiagramm zur Konstruktion der Transformationskurve ermittelt man die Allokation der Faktoren.

Wichtig ist der Hinweis, dass Punkte unterhalb der Großen Nutzenmöglichkeitskurve gesellschaftlich wünschenswerter als Punkte auf ihr sein können, denn sie können ja auf einer höheren Bergson-Indifferenzkurve liegen. Diese lassen sich übrigens auch im Güterraum konstruieren. Dazu ermittelt man alle individuellen Nutzenkombinationen, für die die Wohlfahrtsfunktion $W_i = W_i(U_M,U_W)$ einen konstanten Wert $W_0$ annimmt. Zu jeder dieser Nutzenkombinationen gehört eine Scitovsky-Indifferenzkurve im Güterraum. Die innere Grenze all dieser Kurven ist die Bergson-Indifferenzkurve im Güterraum, die die Minimummenge eines Gutes bei vorgegebener Menge des anderen anzeigt, die zur Aufrechterhaltung der vorgegebenen Wohlfahrt $W_0$ erforderlich ist.

Keine Diskussion einer Sozialen Wohlfahrtsfunktion kommt umhin, Arrows Unmöglichkeitstheorem zu erwähnen. Wir haben bisher die Bergson-Wohlfahrtsfunktion eines rationalen Individuums betrachtet, die wir als persönlich, sozial, paretianisch und individualistisch charakterisiert haben. Arrows untersuchte, ob sich die persönlichen Wohlfahrtsfunktionen zu einer gemeinsamen Wohlfahrtsfunktion $W$ für alle $n$ Mitglieder einer sozialen Gruppe aggrgieren lassen.

Wenn wir bisher nur die Wohlfahrtsfunktion des Individuums i als maßgeblich für die Beurteilung der Situation der Gesellschaft ansahen, war i in gewisser Hinsicht ein Diktator. Indem wir i rationales Verhalten unterstellten, erhielten wir eine in sich schlüssige Soziale Wohlfahrtsfunktion. Arrow stellte sich nun die Frage, ob solche logische Konsistenz auch bei kollektiven Beurteilungsverfahren möglich ist, bei denen die Präferenzen einer Vielzahl von Personen - i.d.R. aller Mitglieder der Gesellschaft - Berücksichtigung finden sollen.

Unter gewissen Bedingungen, die Arrow zugrunde legte, lautet die Antwort nein. Die Einführung der Bedingungen hat folgenden Grund: Will sich eine Gesellschaft auf eine Soziale Wohlfahrtsfunktion einigen, benötigt sie dafür eine (Wahl)Regel. Für die Einigung auf eine Regel benötigt sie jedoch bereits eine Regel usw. Um den sich ergebenden unendlichen Prozess zu vermeiden, werden Bedingungen für eine solche Regel axiomatisch gesetzt. Diese Bedingungen nach Arrow stellen wir hier vor (für weitergehende Betrachtungen sei allerdings auf die Literatur verwiesen).

Ausgangspunkt für Arrows Unmöglichkeitstheorem ist die Annahme, alle Individuen besäßen eine schwache, d.h. Indifferenzmöglichkeiten einschließende Präferenzordnung, die reflexiv, vollständig und transitiv ist. Arrow zeigt, dass keine Aggregationsregel existieren kann, die den folgenden vier Bedingungen genügt und eine Soziale Präferenzordnung erzeugt, die ebenfalls vollständig, reflexiv und transitiv ist:

1. 1. Unbeschränktheit der individuellen Präferenzen

Diese Bedingung besagt, dass jedermann seinen Nutzen nach eigenem Ermessen einschätzen soll. Alle logisch möglichen individuellen Präferenzordnungen sind zugelassen. Frei interpretiert könnte man von einem Recht auf Meinungsfreiheit sprechen.

1. 2. Schwache Pareto-Bedingung

Ziehen alle Individuen Alternative x Alternative y streng vor, so soll auch in der sozialen Präferenzordnung x streng y vorgezogen werden. Zusammen mit der ersten Bedingung folgt, dass eine soziale Präferenzordnung nicht von außen auferlegt sein soll.

1. 3. Unabhängigkeit von irrelevanten Alternativen

Die kollektive Wahl zwischen zwei Alternativen x und y hängt nur von deren relativen Stellungen in den einzelnen Präferenzordnungen ab. Wird zwischen diesen beiden Alternativen gewählt, dann soll das Ergebnis unbeeinflusst bleiben von dritten Alternativen, die nicht zur Wahl stehen. Die Bedingung hat die beiden wichtigen Konsequenzen, dass die Sozialwahlfunktion vom Abstimmungstyp sein muss und Intensitäten von und zwischen Alternativen unberücksichtigt bleiben. Sie ist die umstrittenste der vier Bedingungen.

1. 4. Nicht-Diktator Bedingung

Es gibt kein Individuum, dessen Präferenzordnung unabhängig von den Präferenzen der anderen automatisch die soziale Präferenzordnung darstellt. Diese Bedingung verbrieft also ein Selbstbestimmungsrecht.

Insgesamt lassen sich die Bedingungen als eine Minimalnorm für Verfassungen interpretieren. Arrow beweist, dass keine Verfassung existiert, die alle vier Bedingungen zugleich erfüllt. Als unumstritten gilt die Bedeutung dieses Unmöglichkeitstheorems für die praktische Politik - man denke nur an das bekannte suche Condorçet-Abstimmungsparadox, wo bereits bei drei Wählern und drei (streng geordneten) Alternativen in 12 von 216 möglichen Fällen zyklisch soziale Präferenzen auftreten. Zwar steigt die Wahrscheinlichkeit von Intransivitäten rasch mit der Zahl von Wählern und Alternativen, jedoch bleibt zu bedenken, dass das Unmöglichkeitstheorem bei vielen Entscheidungsprozessen keine Rolle spielt, da seine Bedingungen nicht gegeben sind.

|           | Impressum